我们都知道,实数包括有理数和物理学,每个实数与数轴上的点一一对应。

不过,或许我们对“无理数”的定义本身就带有偏见,总是会下意识地认为无理数就是“无理”的,实际上,有理数与无理数是平等的,都是真实存在的数,也是确定的数。
但是,由于无理数是无限不循环的数,很多人并不太好接受无限的概念。甚至有理数的无限循环也很难接受。
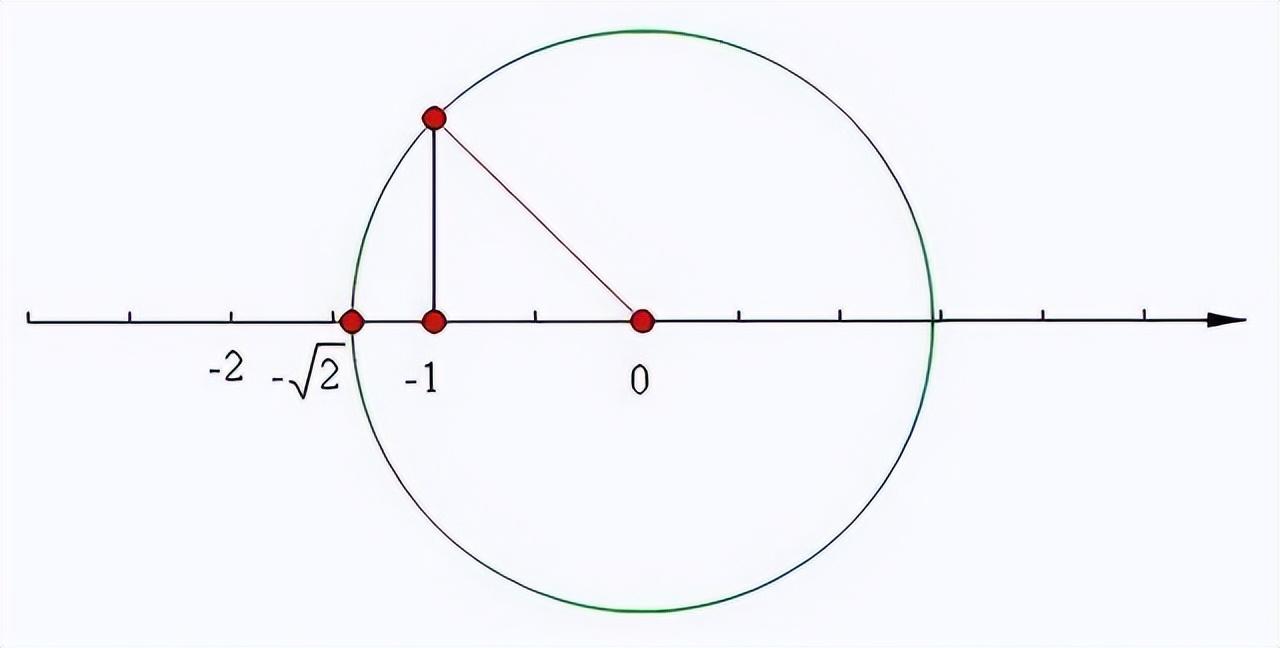
比如很多人经常会问这类问题:1/3等于0.333...,既然除不尽,那么1米长的棍子能否分成三等份?
这个问题就涉及到我们对无穷的理解了。
最简单的问题:1/3为什么非得小数表示,非得要除尽呢?
我想说的是,1/3就是1/3,如同1就是1一样。1/3虽然用小数表示时除不尽,但并不妨碍它是一个准确的数,确定的数。正是因为1/3是确定的数,因此1米长的棍子当然能被分成三等份,每份的长度就是1/3米。
实际上,一根棍子不但能被分成三等份,还能截取一段π米的长度!

说到这里,肯定有人会不服气,π是无限不循环小数,怎么可能有π米长度的棍子存在呢?
其实,上述问题反映的本质是,认为π不是一个确定的数,是一个模糊的数,因为π不能用小说完全表述出来,也不是无限循环小说。
正如我刚开始所讲,其实这就是对无理数的误解。还是那句话:为什么非得用小数去描述无理数呢?这没有道理。

很多人会提出这样看似合理的要求:你能把π完全写出来吗?
答案是:能!而且很简单,直接写“π”就可以了!
有人可能会反驳:我让你用小数把π写出来,谁让你直接写π了?
答案我已经说很多遍了:为什么一定要用小数表示出来呢?π就是π,非常确定的数,就如同“1就是1,也是非常确定的数”一样!
既然π是确定的数,当然存在π米长度的棍子了!就如同存在1米长度的棍子一样!
说白了,只要1米长度的棍子,一定存在π米长度的棍子,不接受反驳!
因为无理数与有理数本来就是对等的,在数轴上都是对应的某个点,难道数轴上的点还有优劣之分吗?有理数就高出无理数一头?
这完全没有道理!

说白了,问题的本质就是0.999......等于1。如果你理解不了为什么,就会有很多疑问。如果你理解了为什么0.999......等于1,就不会有任何问题。
可能我说得有些啰嗦了,但有些东西就需要反复强调,才能打破很多人心目中的固有思维模式。
再举个例子,很多人会想不通,比如说一个圆的直径是1米,那么周长就是π米,于是就问:圆的周长怎么可能是π米呢?甚至认为π米就是不确定的长度!
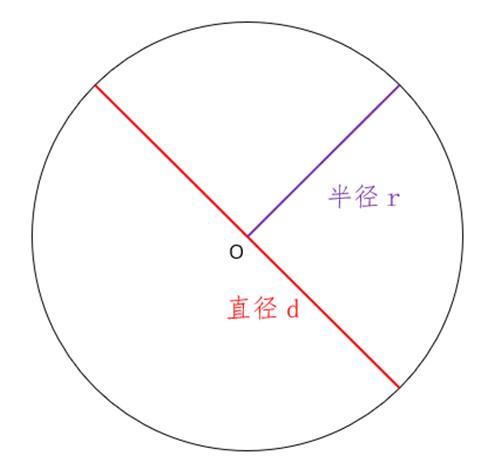
怎么可能就不是π米呢?π米是真实存在的确定的长度!
当然,以上只是单纯从数学概念上去分析,实际上现实中你不可能把1米长度的棍子分成三等份,这就是数学与物理的区别!









相关文章